二叉树遍历

二叉树遍历主要为前序、中序、后序，以及层序四种遍历方式；而前三者的实现上又可分为递归实现和非递归实现，两种方式都要熟练运用。

递归版本

二叉树的前中后序遍历是二叉树结构的最基本算法，采用递归的写法可以快速，简洁地实现该功能，但同时，由于递归方法过于简单，面试中往往会考察非递归版本。

我们先来看下二叉树节点的结构：

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int x) { val = x; }
}

我们可以先来看下二叉树各种遍历顺序：

其实很好记，就是中间节点在最前面、中间和最后面输出，而左右的相对顺序是固定的。

我们来看个图，可能会更加直观一些：

先序遍历顺序：

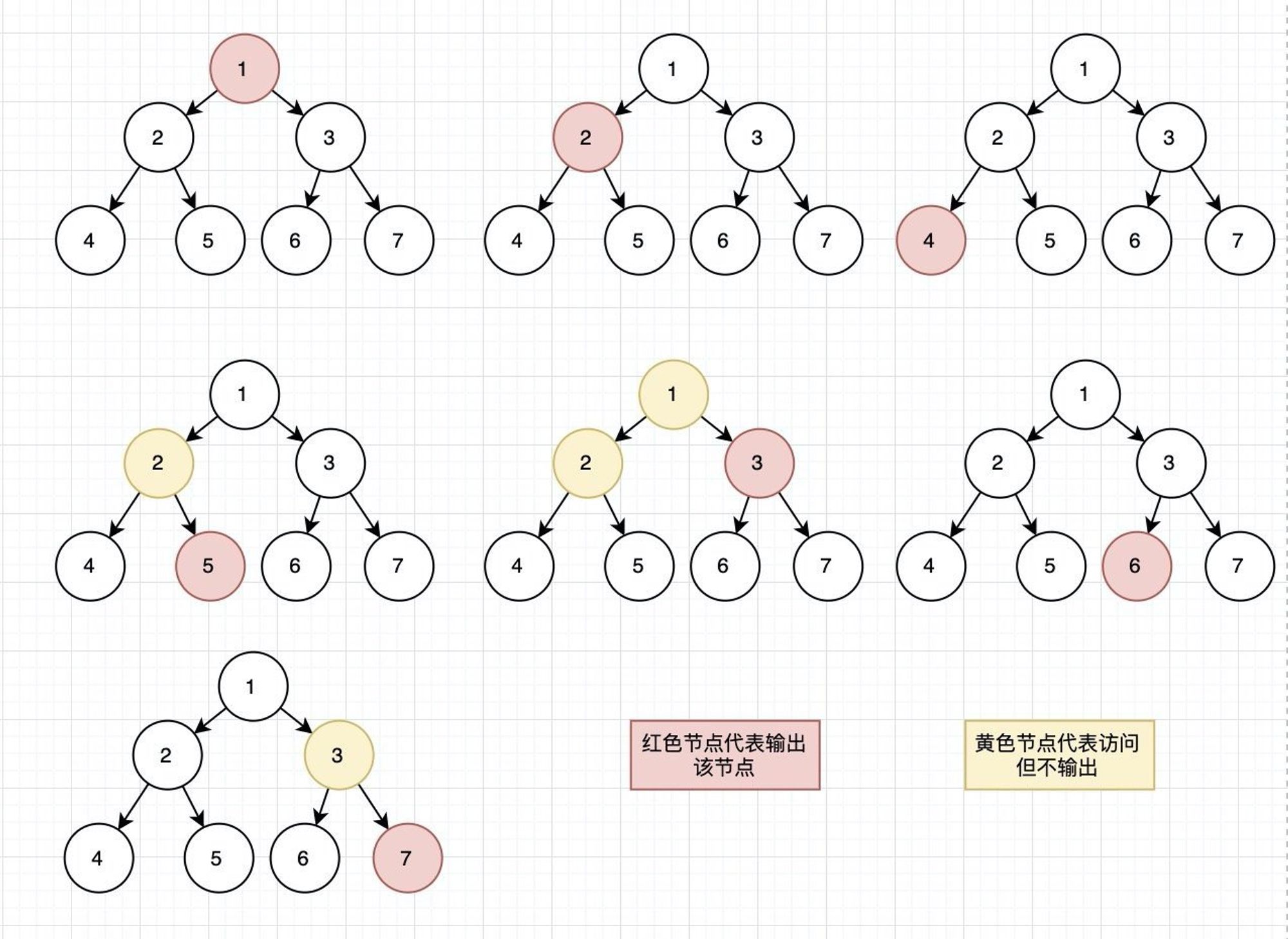
中序遍历顺序：

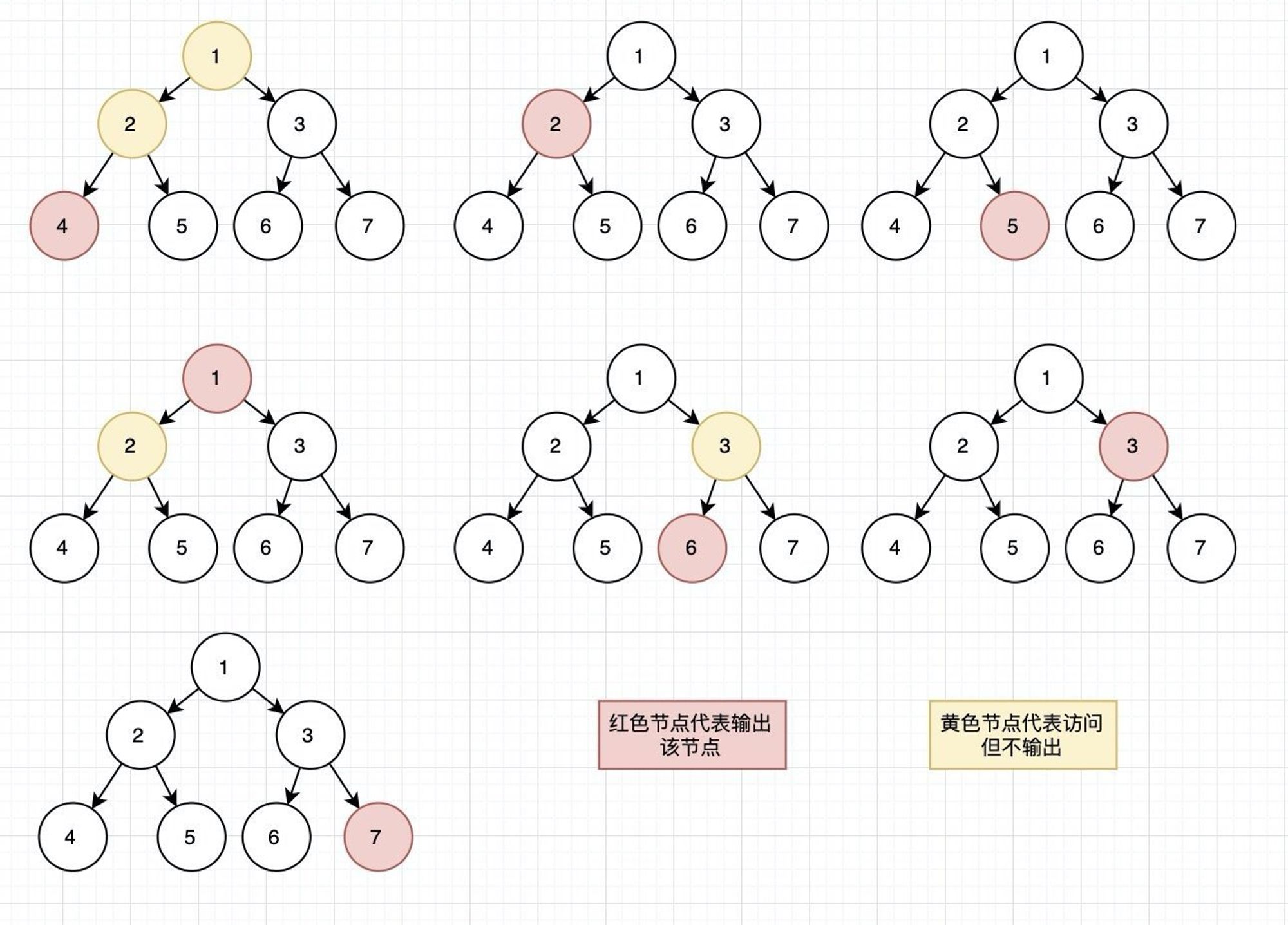
后序遍历顺序：

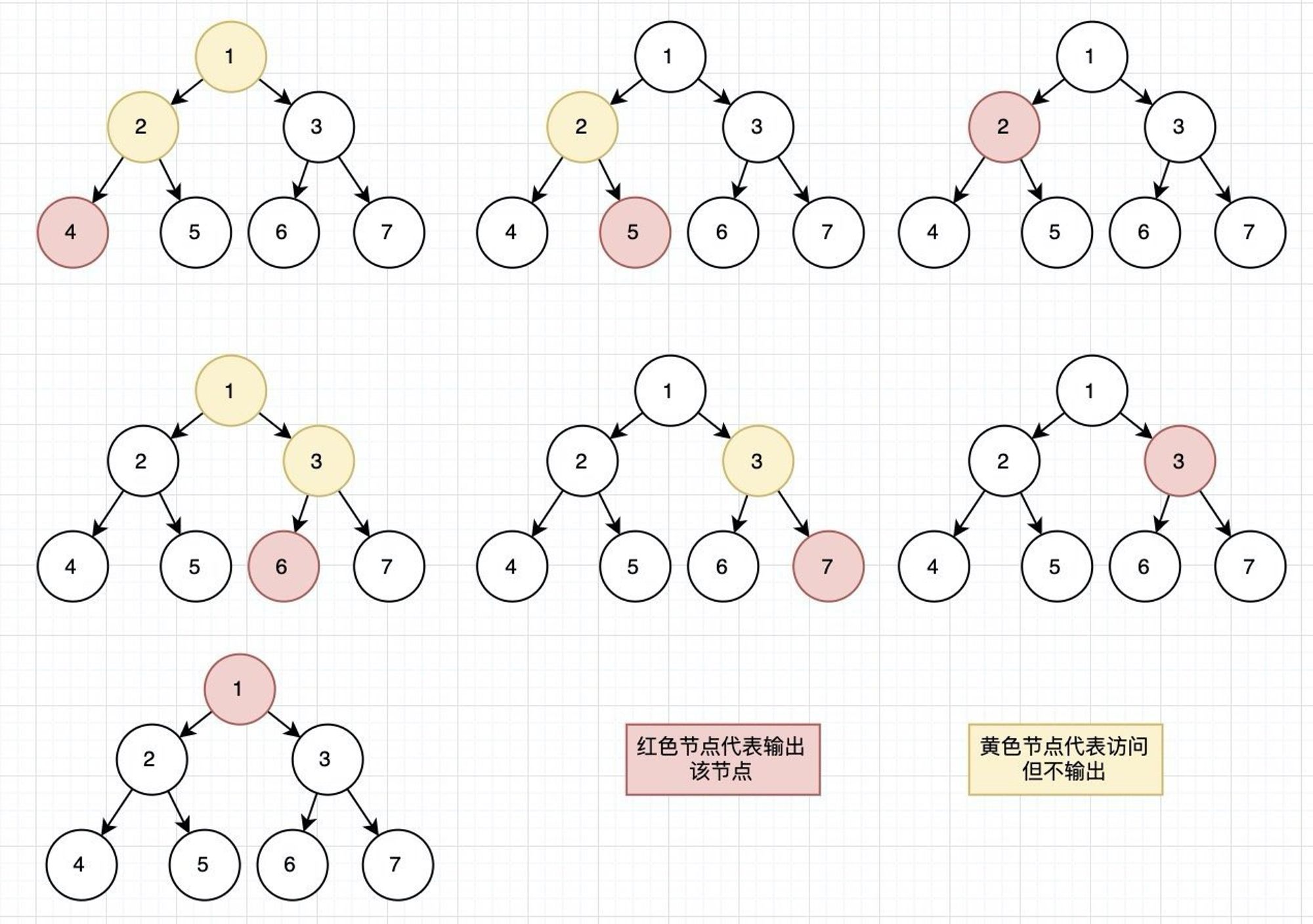
递归版本代码实现：

先序遍历：

public void preOrder(TreeNode root) {
    if (root == null)
        return;
    System.out.print(root.val + " "); // 输出控制
    preOrder(root.left);
    preOrder(root.right);
}

而中序遍历和后序遍历则只需修改输出控制的位置：

中序遍历：

public void inOrder(TreeNode root) {
    if (root == null)
        return;
    inOrder(root.left);
    System.out.print(root.val + " "); // 输出控制
    inOrder(root.right);
}

后序遍历：

public void postOrder(TreeNode root) {
    if (root == null)
        return;
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.val + " "); // 输出控制
}

非递归版本

对于非递归版本，我们要熟悉栈的特性，在把递归函数转化为非递归函数的过程中，如何把握压栈弹栈的时机就很关键。

先序遍历：

如下图所示，蓝色代表入栈，红色代表出栈并且输出；

一开始先把根节点压栈，每次取栈顶元素的同时输出该元素，然后把栈顶元素的右孩子、左孩子分别入栈（如果有的话，为空则不用）；直到栈为空则停止。

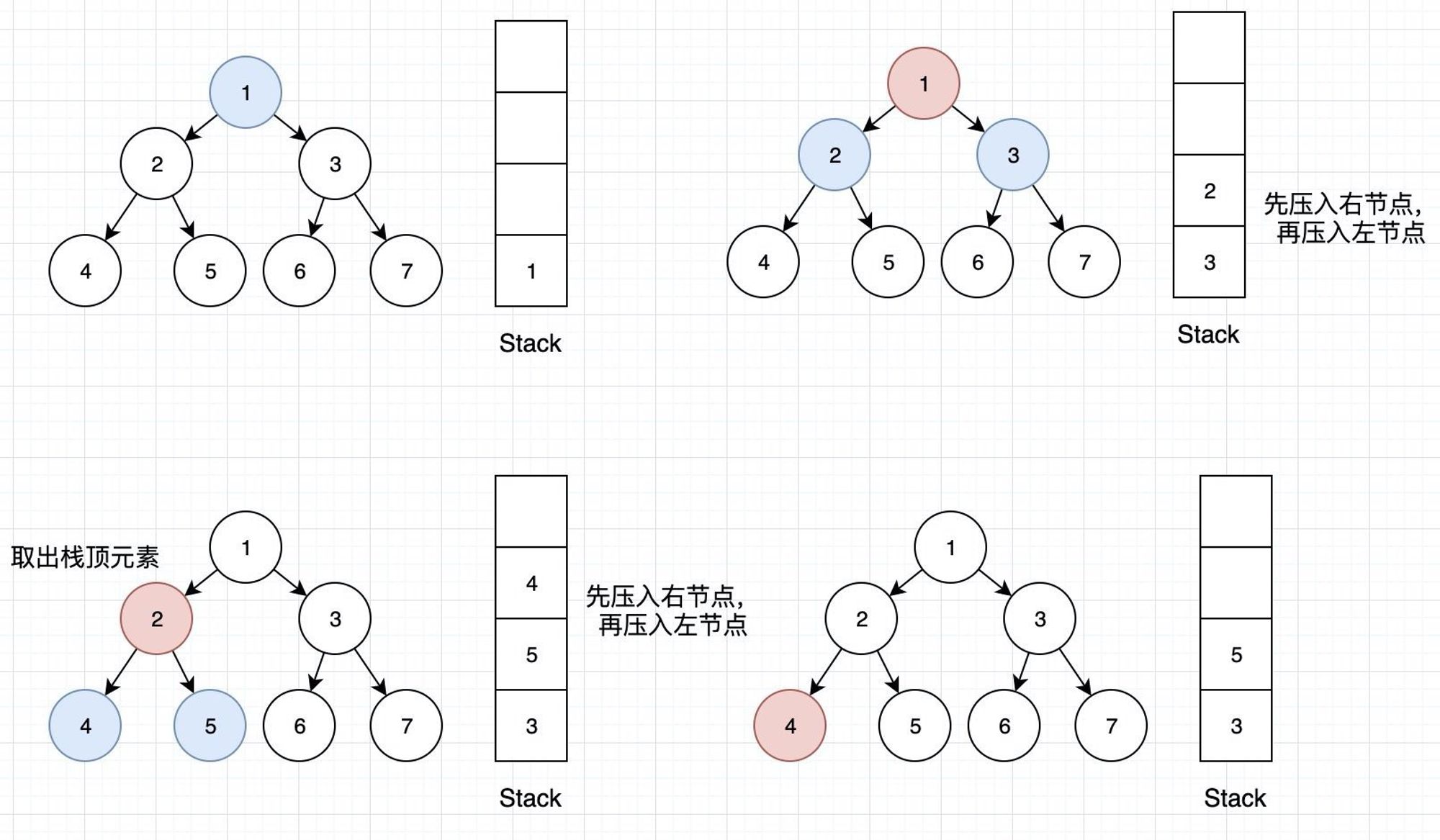
代码如下：

public List<Integer> preOrderByStack(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    if (root == null) // 边界判断
        return res;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        root = stack.pop(); // 输出当前栈顶元素
        res.add(root.val);
        if (root.right != null) // 先压入右孩子
            stack.push(root.right);
        if (root.left != null) // 再压入左孩子
            stack.push(root.left);
    }
    return res;
}

后序遍历：

这里为什么不先讲中序遍历呢？因为后序遍历有一种非常trick的做法，我们知道先序遍历为中左右，而后序遍历为左右中，我们把后序遍历反过来，就是中右左，是不是发现和先序遍历有点像了？我们先序遍历采用了先压入右孩子再压入左孩子的方式得到了中左右的顺序，那么我们只要先压入左孩子，再压入右孩子，就能得到中右左的顺序，这里只要存的时候从前往后插入，就变成了我们想要的后序遍历了：左右中。

public List<Integer> postOrderByStack(TreeNode root) {
    LinkedList<Integer> res = new LinkedList<>();
    if (root == null)
        return res;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        root = stack.pop();
        res.addFirst(root.val); // 从前往后插入，相当于调转列表
        if (root.left != null)
            stack.push(root.left);
        if (root.right != null)
            stack.push(root.right);
    }
    return res;
}

中序遍历：

我们知道中序遍历的顺序是左中右，我们通过前面递归版本的情况可以了解到，对于某个节点来说，如果其左孩子存在，那么我们就得先打印其左孩子，反映到代码中，我们的当前节点只要有左孩子，就将其左孩子压栈，并且当前节点向其左孩子方向移动，直到当前节点为空，说明此时位于最左下方的节点的空左孩子处，那么接下来我们就需要弹栈获取栈顶，输出元素，然后移动到栈顶节点的右孩子处，结合下图理解过程：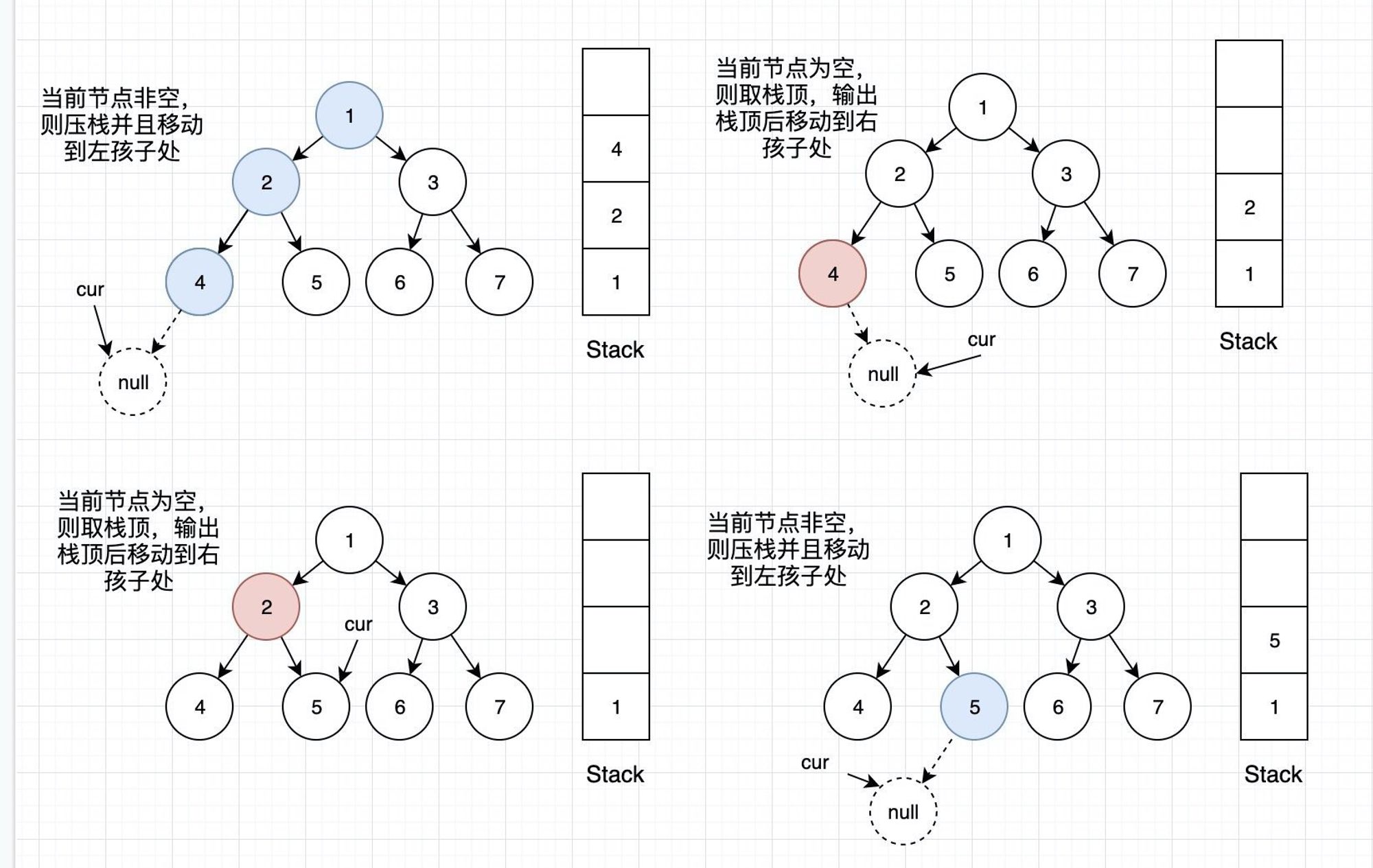

我们再结合代码看看：

public List<Integer> inOrderByStack(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    while (!stack.isEmpty() || (root != null)) {
        if (root != null) { // 当前节点非空，压栈后向左移动
            stack.push(root);
            root = root.left;
        } else { // 当前节点为空，弹栈输出后向右移动
            root = stack.pop();
            res.add(root.val);
            root = root.right;
        }
    }
    return res;
}

层序遍历

简单来说就是一行一行地遍历，基于队列来做，先把根节点入队列，只要队列非空，每次把队头结点弹出，然后把堆头的左右孩子压入队列中，这样最终遍历出来的就是层序遍历的顺序。

public List<Integer> levelOrder(TreeNode root) {
    if (root == null)
        return null;
    List<Integer> res = new ArrayList<>();
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root); // 先把根节点入队列
    while (!queue.isEmpty()) { // 队列非空
        root = queue.poll();
        res.add(root.val); // 弹出队头节点
        if (root.left != null) queue.add(root.left);
        if (root.right != null) queue.add(root.right);
    }
    return res;
}