1. 高楼扔鸡蛋问题
有一栋楼共
100层,一个鸡蛋从第N层及以上的楼层落下来会摔破, 在第N层以下的楼层落下不会摔破。给你2个鸡蛋,如何用最少的尝试次数,测试出鸡蛋不会摔碎的临界点?首先要说明的是这道题你要是一上来就说出正确答案,那说明你的智商不是超过160就是你做过这题。
所以建议你循序渐进的回答,一上来就说最优解可能结果不会让面试官满意。
1. 暴力法
从
1到100,一层一层试。在最坏情况下,这个方法需要扔100次。 这个办法太蠢了,完全用不上两个鸡蛋这个条件,不建议回答这个方法。2. 二分法
采用类似于二分查找的方法,把鸡蛋从一半楼层(
50层)往下扔。- 如果第一枚鸡蛋,在
50层碎了,第二枚鸡蛋,就从第1层开始扔,一层一层增长,一直扔到第49层。
- 如果第一枚鸡蛋在
50层没碎,则继续使用二分法,在剩余楼层的一半(75层)往下扔......
这个方法在最坏情况下,需要尝试
50次。3. 均匀法
如何让第一枚鸡蛋和第二枚鸡蛋的尝试次数,尽可能均衡呢?
很简单,做一个平方根运算,
100的平方根是10。因此,我们尝试每
10层扔一次,第一次从10层扔,第二次从20层扔,第三次从30层......一直扔到100层。这样的最好情况是在第
10层碎掉,尝试次数为 1 + 9 = 10次。最坏的情况是在第
100层碎掉,尝试次数为 10 + 9 = 19次。不过,这里有一个小小的优化点,我们可以从
15层开始扔,接下来从25层、35层扔......一直到95层。这样最坏情况是在第
95层碎掉,尝试次数为 9 + 9 = 18次。4. 最优解法
最优解法是反向思考的经典:如果最优解法在最坏情况下需要扔
X次,那第一次在第几层扔最好呢?答案是:从
X层扔假设最优的尝试次数的
x次,为什么第一次扔就要选择第x层呢?这里的解释会有些烧脑,请小伙伴们坐稳扶好:
- 假设第一次扔在第
x+1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x层。
这样一来,我们总共尝试了
x+1次,和假设尝试x次相悖。由此可见,第一次扔的楼层必须小于x+1层。- 假设第一次扔在第
x-1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第
1层开始一层一层扔,一直扔到第x-2层。这样一来,我们总共尝试了
x-2+1 = x-1次,虽然没有超出假设次数,但似乎有些过于保守。- 假设第一次扔在第
x层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第
1层开始一层一层扔,一直扔到第x-1层。这样一来,我们总共尝试了
x-1+1 = x次,刚刚好没有超出假设次数。因此,要想尽量楼层跨度大一些,又要保证不超过假设的尝试次数x,那么第一次扔鸡蛋的最优选择就是第
x层。那么算最坏情况,第二次你只剩下
x-1次机会,按照上面的说法,你第二次尝试的位置必然是X +(X-1);以此类推我们可得:
x + (x-1) + (x-2) + ... + 1 = 100这个方程不难理解:
左边的多项式是各次扔鸡蛋的楼层跨度之和。由于假设尝试
x次,所以这个多项式共有x项。右边是总的楼层数
100。下面我们来解这个方程:
x + (x-1) + (x-2) + ... + 1 = 100 转化为 (x+1)*x/2 = 100最终x向上取整,得到
x = 14因此,最优解在最坏情况的尝试次数是
14次,第一次扔鸡蛋的楼层也是14层。最后,让我们把第一个鸡蛋没碎的情况下,所尝试的楼层数完整列举出来:
14,27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100- 举个栗子验证下:
假如鸡蛋不会碎的临界点是
65层,那么第一个鸡蛋扔出的楼层是14,27,50,60,69。这时候啪的一声碎了。第二个鸡蛋继续,从
61层开始,61,62,63,64,65,66,啪的一声碎了。因此得到不会碎的临界点
65层,总尝试次数是 6 + 6 = 12 < 14 。下面是我个人的理解:这个更像是优化版的均匀法,均匀法让你第二次尝试不超过
10,但是第一次的位置无法保证(最多要9次,最好一次),这个由于每多一次尝试,楼层间隔就-1,最终使得第一次与第二次的和完全均匀(最差情况)。但是核心思路是逆向思考,因为即使理解了需要两次的和均匀也很难得到第一次要在哪层楼扔。
一旦理解了这种方法,多少层楼你都不会怕啦~
2. 找砝码问题
有一个天平,九个砝码,一个轻一些,用天平至少几次能找到轻的?
三分法。
答案:2次。
- 分三份,两份比较,第三份放一边,如果两份相等质量,则说明轻的在第三份。
- 不论如何,可以确定轻的砝码在某一份的三个之中,再用一次三分法,即可确定。
3. 找玻璃球问题
有十组玻璃球,每组十个,每个玻璃球重
10g,但其中有一组玻璃球每个只有9g,给你一个能显示克数的秤,问你最少几次能找到轻的那一组砝码?将十组玻璃珠编号
1~10,然后第一组拿一个,第二组拿两个以此类推...第十组拿十个
将这些玻璃珠一起放到秤上称出克数x,则
y = 1*10 + 2*10 + 3*10 + ... + 10 * 10 - x等价于
y = (1 + 2 + 3 + ... + 10) * 10 - x = 550 - x第
y组就是轻的那组。4. 毒药问题
1000瓶水,其中有一瓶可以无限稀释的毒药,小白鼠喝了毒水就会死(不论含量多低)。要快速找出哪一瓶有毒,需要几只小白鼠?二进制思路。
答:
2^10 = 1024 > 1000,因此10只小白鼠即可。给
1000瓶水按照二进制编号,比如3号编为00000 00011,拿10个碗,对应10位,对于3号水来说,最后两位是1,则把水混合进最后两个碗中。
最终把10碗水给对应的小白鼠喝,根据最后小白鼠死亡的情况(死即为1,活即为0),即可确定出有毒的那碗水。5. 生成随机数问题
给定生成
1到5的随机数Rand5(),如何得到生成1到7的随机数函数Rand7()?- 使用
rand5()生成rand7()
// 需要随机得到 1-7
public static int rand7() {
while (true) {
int row, col, idx;
// rand5() 返回 1-5
row = rand5(); // 5 * 5 = 25, 设想一个 5*5 的矩阵
col = rand5(); // 然后找到小于25的,7的最大倍数21
idx = col + (row - 1) * 5;
if (idx <= 21) // 只考虑 1-21,划分成 7 份
return 1 + (idx - 1) % 7;
}
}6. 先手必胜策略问题:
100本书,每次能够拿1-5本,怎么拿能保证最后一次是你拿?
- 卡关键点,每次只能拿
15本,所以当剩下6本的时候,不论对面怎么拿你都能赢;
- 然后推
6的倍数:12、18、...、96,也就是一开始要拿4本;
- 接下来对面拿
1,你就拿5,对面拿2,你就拿4,总之让你拿的和对面拿的加起来是6,最终就能赢。
- 推广到
n本书,每次拿1-k本,怎么保证最后一次是你拿?
7. 瓶子换饮料问题
1000瓶饮料,3个空瓶子能够换1瓶饮料,问最多能喝几瓶?1000 % 3 = 333...1喝掉1000瓶,可以换333瓶汽水, 余1个空瓶
333 % 3 = 111...0喝掉333瓶,可以换111瓶汽水, 余0个空瓶
111 % 3 = 37...0喝掉111瓶,可以换37瓶汽水, 余0个空瓶
37 % 3 = 12...1喝掉37瓶,可以换12瓶汽水, 余1个空瓶
12 % 3 = 4...0喝掉12瓶,可以换4瓶汽水, 余0个空瓶
4 % 3 = 1...1喝掉4瓶,可以换1瓶汽水, 余1个空瓶
- 此时剩下
1瓶汽水 +3个空瓶,其中3个空瓶可以再换1瓶
- 此时剩下
2瓶,喝掉2瓶,不能再换了。 总共:1000 + 333 + 111 + 37 + 12 + 4 + 2 = 1499瓶
8. 重合问题
在一天的
24小时之中,时钟的时针、分针和秒针完全重合在一起的时候有几次?都分别是什么时间?- 假设时针的角速度为
ω(ω = 1 / 120 (度/秒)),那么分针的角速度就为12ω,秒针的角速度为720ω
- 假设时针和分针在
t秒后重合,那么分针在t时间内走过的角度减去时针在t时间内走过的角度,得到的结果肯定是360的整数倍
- 根据上面的规则,可以算出时针和分针重合的时间 – 集合
A
- 同理也能算出分针和秒针重合的时间 – 集合
B
- 那么时针、分针及秒针三者重合的时间就是集合
A、B的交集
结果:
A.length = 22
B.length = 1416
A ∩ B = ['00:00:00', '12:00:00'] = 2
9. 赛马问题(腾讯高频)
- 有
25匹马,每场比赛只能赛5匹,找最快的3匹马,至少要赛多少场?
- 有
64匹马,每场比赛只能赛8匹,找最快的4匹马,至少要赛多少场?
- 有
25匹马,每场比赛只能赛5匹,找最快的5匹马,至少要赛多少场?
25匹马5条跑道找最快的3匹马,需要跑几次?答案:7次
64匹马8条跑道找最快的4匹马,需要跑几次?答案:最少10次,最多11次
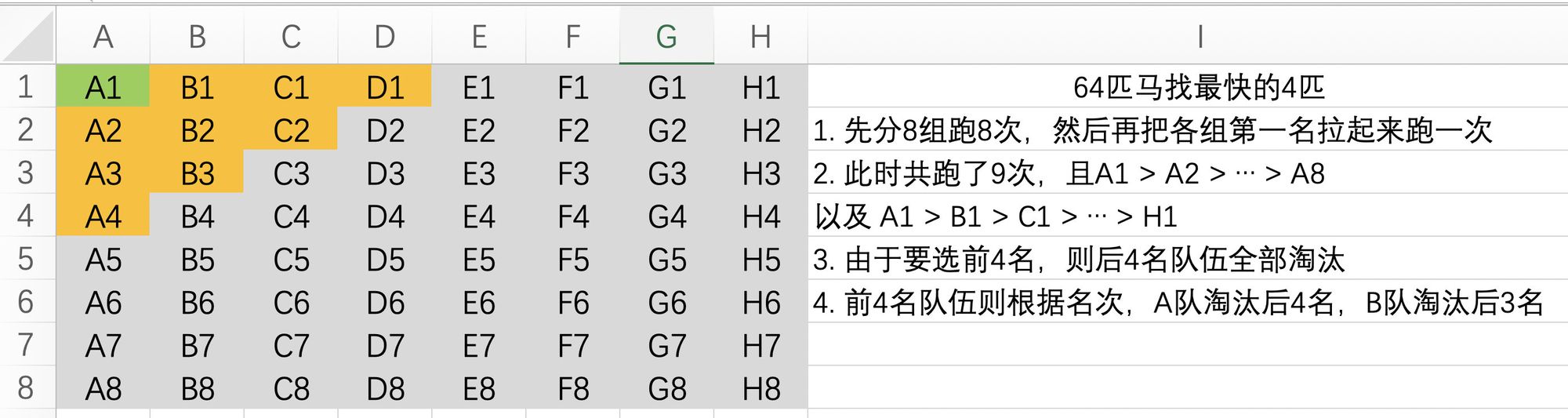
此时
A1显然是第一名,接下来需要找出第2、3、4名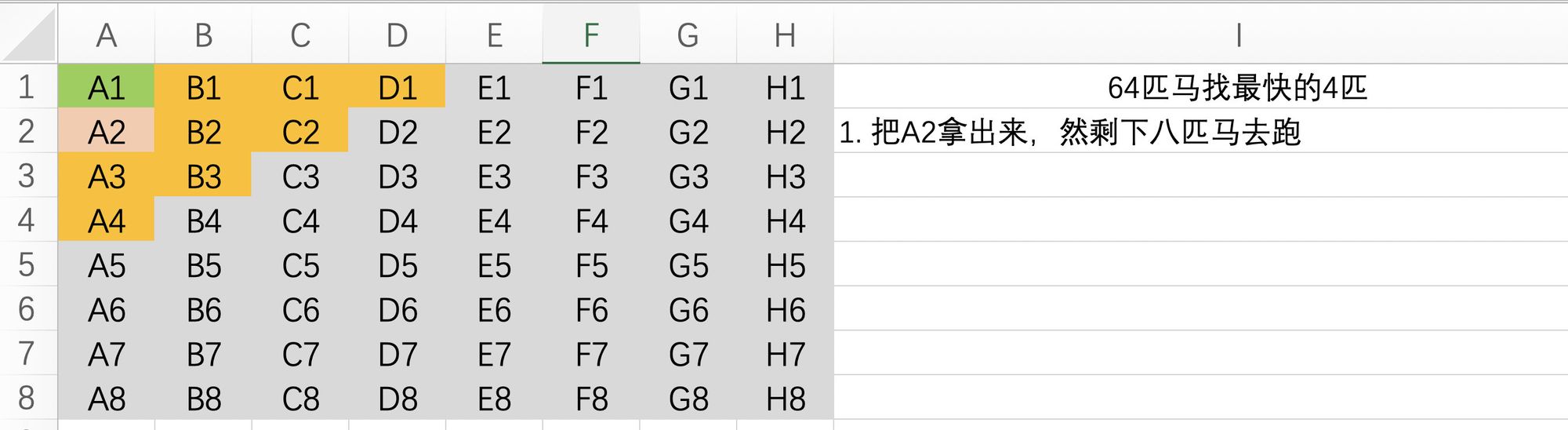
如果
A3拿了第一名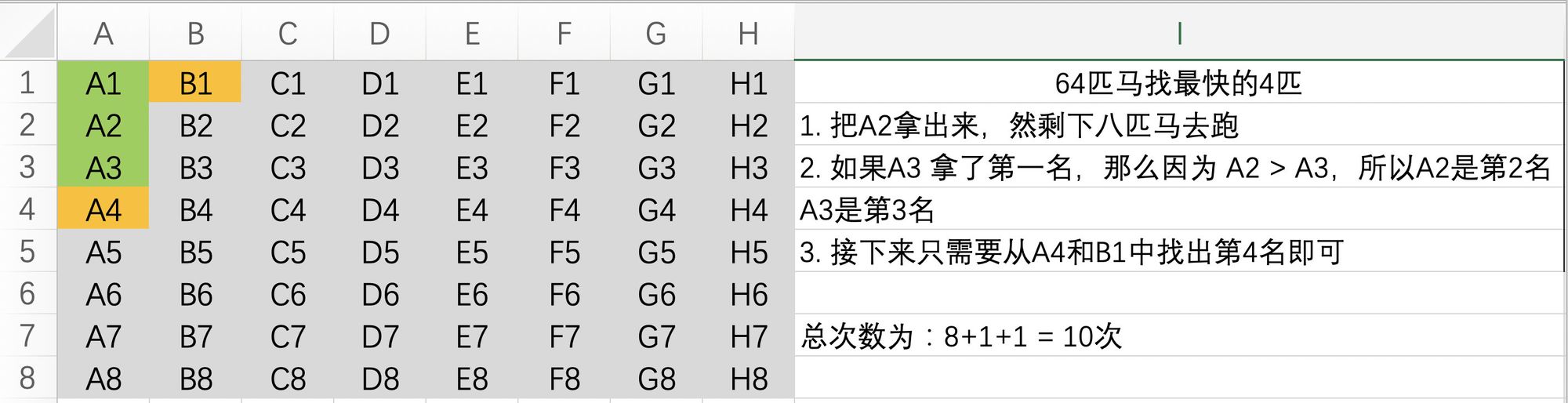
如果
A3不是第一,也就是说B1拿了第一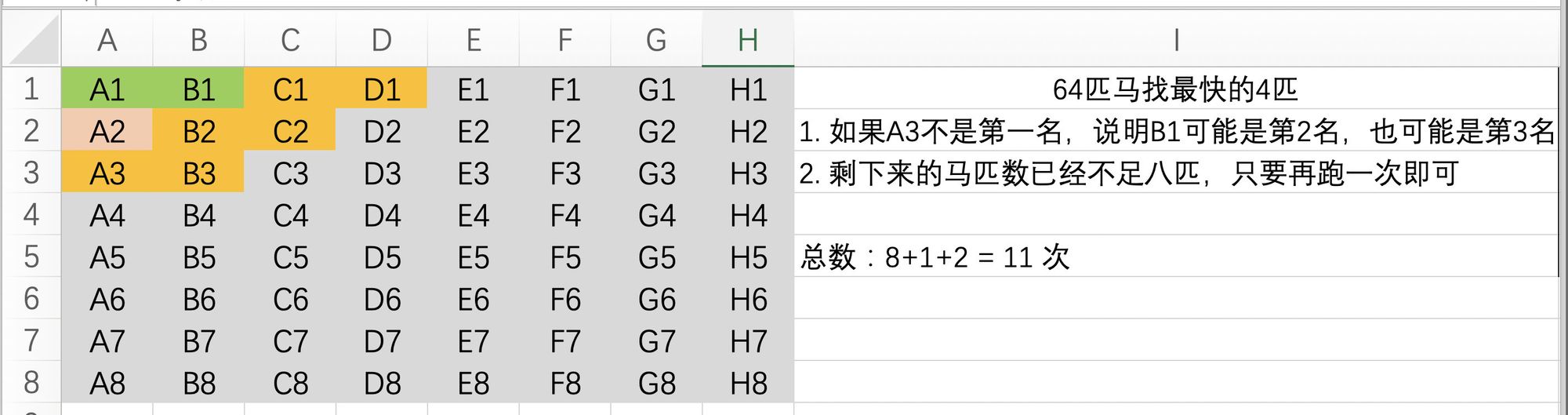
25匹马5条跑道找最快的5匹马,需要跑几次?答案:最少8次,最多9次
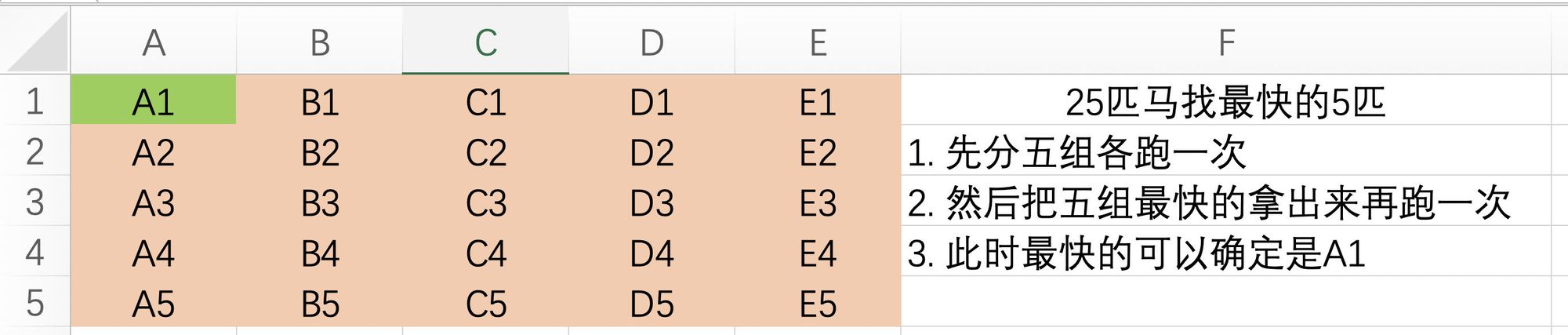
现在已经跑了
5 + 1=6次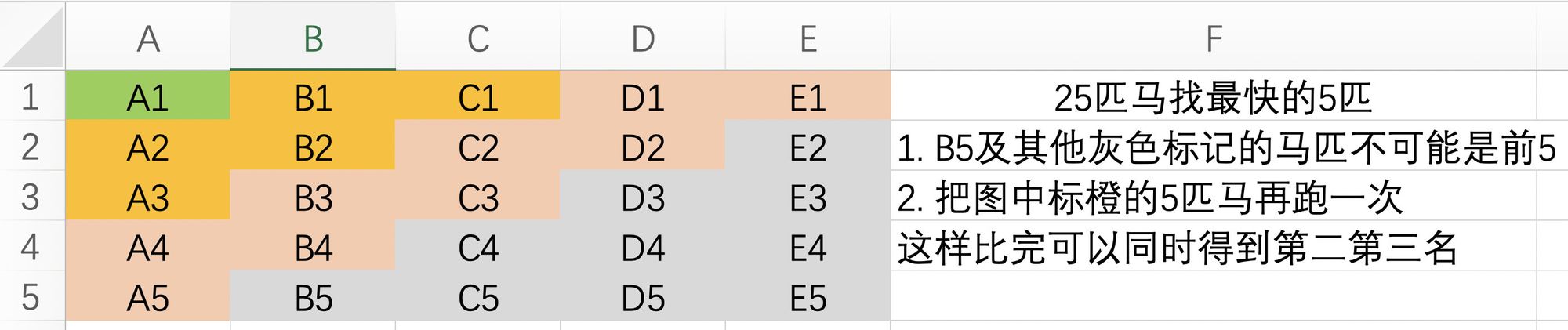
现在已经跑了
5 + 1 + 1 = 7次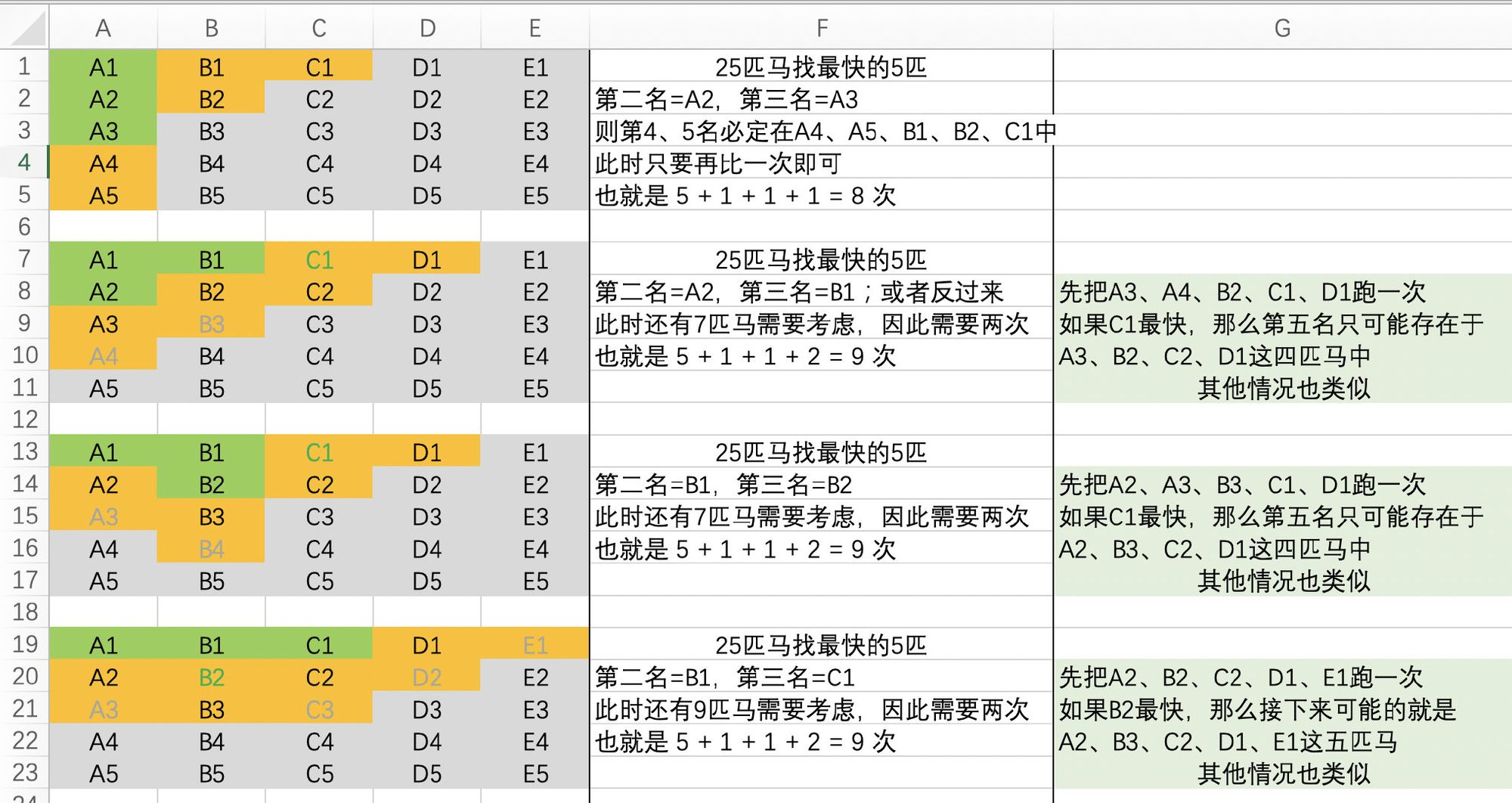
10. 烧香确定时间问题
有两根不均匀的香,燃烧完都需要一个小时,问怎么确定
15分钟的时长?相对时间的思路。
答:设两根香分别为
A、B,先把A一端点燃,然后把B的两端都点燃,这样当B烧完的时候,A就还剩下一半(此时能确定半小时),此时把A的另一端也点燃,那么从此刻到A烧完的时间就是15分钟。11. 掰巧克力问题
N*M块巧克力,每次掰一块的一行或一列,掰成1*1的巧克力需要多少次?
- 淘汰问题:
1000个人参加辩论赛,1V1,输了就退出,需要安排多少场比赛?
- 每次拿起一块巧克力,掰一下(无论横着还是竖着)都会变成两块,因为所有的巧克力共有
N*M块,所以要掰N*M-1次,减1是因为最开始的一块是不用算进去的。
- 每一场辩论赛两个人,淘汰一个人,所以可以看作是每一场辩论赛减少一个人,直到最后剩下
1个人,所以是1000 - 1 = 999场。
参考
- [代码不规范,测试两行泪]: https://www.nowcoder.com/discuss/262595
- [青青子衿]: https://hexuanzhang.github.io/






Loading Comments...